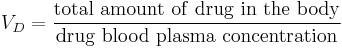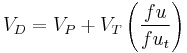Volume of distribution

The volume of distribution (V_D) , also known as apparent volume of distribution, is a pharmacological term used to quantify the distribution of a medication between plasma and the rest of the body after oral or parenteral dosing. It is defined as the theoretical volume in which the total amount of drug would need to be uniformly distributed to produce the desired blood concentration of a drug.^[1] ^[2]

Volume of distribution may be increased by renal failure (due to fluid retention) and liver failure (due to altered body fluid and plasma protein binding). Conversely it may be decreased in dehydration.

The initial volume of distribution describes blood concentrations prior to attaining the apparent volume of distribution and uses the same formula.

1 Equations
2 Examples
3 Sample values and equations
4 References
5 External links

Equations

The volume of distribution is given by the following equation:

${V_{D}} = \frac{\mathrm{total \ amount \ of \ drug \ in \ the \ body}}{\mathrm{drug \ blood \ plasma \ concentration}}$

Therefore the dose required to give a certain plasma concentration can be determined if the V_D for that drug is known. The V_D is not a physiologic value; it is more a reflection of how a drug will distribute throughout the body depending on several physicochemical properties, e.g. solubility, charge, size, etc.

The units for Volume of Distribution are typically reported in (ml or liter)/kg body weight. The fact that V_D is a ratio of a theoretical volume to a fixed unit of body weight explains why the V_D for children is typically higher than that for adults, even though children are smaller and weigh less. As body composition changes with age, V_D decreases.

The V_D may also be used to determine how readily a drug will displace into the body tissue compartments relative to the blood:

${V_{D}} = {V_{P}} %2B {V_{T}} \left(\frac{fu}{fu_{t}}\right)$

Where:

V_P = plasma volume

V_T = apparent tissue volume

fu = fraction unbound in plasma

fu_T = fraction unbound in tissue

Examples

Understanding volume of distribution

If you administer a dose D of a drug intravenously in one go (IV-bolus), you would naively expect it to have an immediate blood concentration 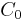$C_0$ which directly corresponds to the amount of blood contained in the body 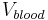$V_{blood}$ . Mathematically this would be:

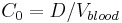
$C_0 = D/V_{blood}$

But this is generally not what happens. Instead you observe that the drug has distributed out into some other volume (read organs/tissue). So probably the first question you want to ask is how much of it is no longer in the blood stream? The volume of distribution 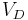$V_D$ quantifies just that by specifying how big a volume you would need in order to observe the blood concentration actually measured.

A practical example for a simple case (mono-compartmental) would be to administer D=8 mg/kg to a human. A human has a blood volume of around 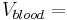$V_{blood}=$ 0.08 l/kg ^[3]. This gives a 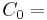$C_0=$ 100 µg/ml if the drug stays in the blood stream only, and thus its volume of distribution is the same as 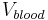$V_{blood}$ that is 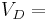$V_D=$ 0.08 l/kg. If the drug distributes into all body water the volume of distribution would increase to approximately 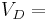$V_D=$ 0.57 l/kg ^[4]

If the drug readily diffuses into the body fat the volume of distribution may increase dramatically, an example is chloroquine which has a 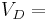$V_D=$ 250-302 l/kg ^[5]

In the simple mono-compartmental case the volume of distribution is defined as: 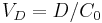$V_D=D/C_0$ , where the 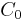$C_0$ in practice is an extrapolated concentration at time=0 from the first early plasma concentrations after an IV-bolus administration (generally taken around 5min - 30min after giving the drug).

Further reading:

Table of volume of distribution for drugs

Drug	V_D	Comments
Warfarin	8L	Reflects a high degree of plasma protein binding.
Theophylline, Ethanol	30L	Represents distribution in total body water.
Chloroquine	15000L	Shows highly lipophilic molecules which sequester into total body fat.
NXY-059	8L	Highly-charged hydrophilic molecule.

Sample values and equations

Characteristic	Description	Example value	Abbreviation(s)	Formula
Dose	Loading dose (LD), or steady state / maintenance dose (MD).	500 mg	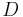$\textstyle D$	design parameter
τ	Dosing interval.	24 h	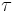$\textstyle \tau$	design parameter
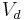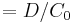Volume of distribution	The apparent volume in which a drug is distributed immediately after it has been injected intravenously and equilibrated between plasma and the surrounding tissues.	6.0 L	$\textstyle V_d$	$\textstyle = D / C_0$
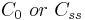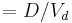Concentration	Initial or steady-state concentration of drug in plasma.	83.3 µg/mL	$\textstyle C_{0} \ or \ C_{ss}$	$\textstyle = D / V_d$
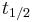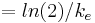Biological half-life	The time required for the concentration of the drug to reach half of its original value.	12 h	$\textstyle t_{1/2}$	$\textstyle = ln (2) / k_{e}$
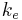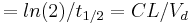Elimination rate constant	The rate at which drugs are removed from the body.	0.0578 h^-1	$\textstyle k_e$	$\textstyle = ln (2) / t_{1/2} = CL / V_{d}$
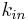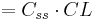Elimination rate	Rate of infusion required to balance elimination.	50 mg/h	$\textstyle k_{in}$	$\textstyle = C_{ss} \cdot CL$
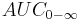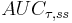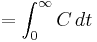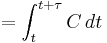Area under the curve	The integral of the concentration-time curve (after a single dose or in steady state).	1320 µg/mL×h	$\textstyle AUC_{0-\infty}$ $\textstyle AUC_{\tau,ss}$	$= \int_{0}^{\infty}C\, dt$ $= \int_{t}^{t%2B\tau}C\, dt$
Clearance	The volume of plasma cleared of the drug per unit time.	0.38 L/h	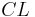$\textstyle CL$	$\textstyle= V_{d} \cdot k_{e} = D/AUC$
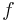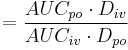Bioavailability	The fraction of drug that is absorbed.	0.8	$\textstyle f$	$= \frac{AUC_{po}\cdot D_{iv}}{AUC_{iv}\cdot D_{po}}$
C_max	The peak plasma concentration of a drug after oral administration.	60.9 µg/mL	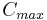$\textstyle C_{max}$	direct measurement
t_max	Time to reach C_max.	3.9 h	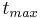$\textstyle t_{max}$	direct measurement
C_min	The lowest (trough) concentration that a drug reaches before the next dose is administered.	27.7 µg/mL	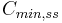$\textstyle C_{min,ss}$	direct measurement
Fluctuation	Peak trough fluctuation within one dosing interval at steady state	41.8 %	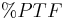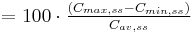$\textstyle�%PTF$	$\textstyle =100 \cdot \frac{(C_{max,ss} - C_{min,ss})}{C_{av,ss}}$ where 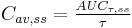$\textstyle C_{av,ss}=\frac{AUC_{\tau,ss}}{\tau}$
edit

References

^ http://www.merckmanuals.com/professional/sec21/ch324/ch324d.html
^ "vetmed.vt.edu". http://cpharm.vetmed.vt.edu/VM8314/VM8314PharmaModeling.htm.
^ Alberts, Bruce (2005). "Leukocyte functions and percentage breakdown". Molecular Biology of the Cell. NCBI Bookshelf. http://www.ncbi.nlm.nih.gov/sites/entrez?cmd=Search&db=books&doptcmdl=GenBookHL&rid=mboc4.table.4143. Retrieved 2007-04-14.
^ Guyton, Arthur C. (1976). Textbook of Medical Physiology (5th ed.). Philadelphia: W.B. Saunders. p. 424. ISBN 0-7216-4393-0.
^ Wetsteyn JC (1995). "The pharmacokinetics of three multiple dose regimens of chloroquine: implications for malaria chemoprophylaxis". Br J Clinical Pharmacology 39 (6): 696–9. PMID 7654492.

External links

Medication > Pharmacology

Pharmacokinetics	ADME: Absorption • Distribution • Metabolism • Excretion (Clearance) Loading dose • Volume of distribution (Initial) • Rate of infusion Compartment • Bioequivalence • Bioavailability Onset of action • Biological half-life • Plasma protein binding Therapeutic index (LD₅₀/ED₅₀)

Pharmacodynamics	Toxicity (Neurotoxicology) • Dose-response relationship (Efficacy, Potency) Antimicrobial pharmacodynamics: Minimum inhibitory concentration/Bacteriostatic • Minimum bactericidal concentration/Bactericide

Agonism and antagonism	Agonist: Inverse agonist • Irreversible agonist • Partial agonist • Superagonist • Physiological agonist Antagonist: Competitive antagonist • Irreversible antagonist • Physiological antagonist Other: Binding • Affinity • Binding selectivity • Functional selectivity

Other	Drug tolerance: Tachyphylaxis Drug resistance: Antibiotic resistance • Multiple drug resistance

Related fields/subfields	Pharmacogenetics • Pharmacogenomics • Neuropsychopharmacology (Neuropharmacology, Psychopharmacology)